From Subsonic to Hypersonic: Understanding Flow Regimes

If you’ve ever wondered why an aircraft looks different once they fly faster than the speed of sound, or why your CFD solver settings change for high-speed flows, you’re in the right place.

Let’s break down what the Mach number is, and more importantly, what it means for the behavior of a fluid.

What is the Mach Number?

In simple terms, the Mach number (M) is the ratio of the speed of an object (or flow) to the speed of sound in that fluid.

Mach Number (M) = Object Speed / Speed of Sound

It’s a dimensionless number, named after the Austrian physicist and philosopher Ernst Mach. This simple ratio is the key that unlocks the door to understanding compressibility effects.

The Speed of Sound: It’s All About Communication

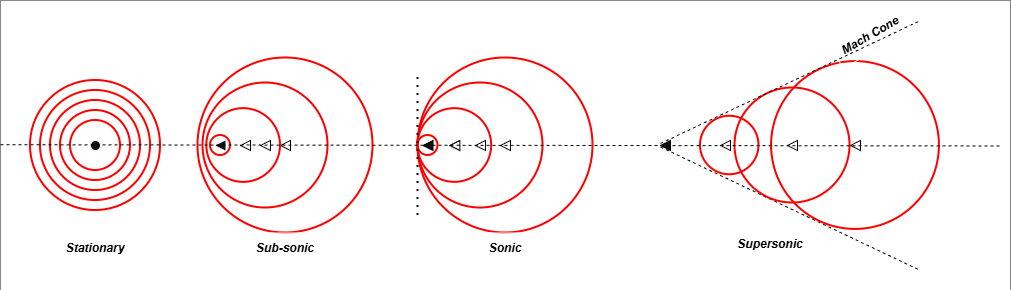
To understand Mach number, you first need to grasp what the “speed of sound” represents. It’s not just the speed at which noise travels; it’s the speed at which information propagates through a fluid.

Imagine a stationary object in a flow. It constantly sends out tiny pressure waves (information) in all directions, telling the incoming fluid particles, “Hey, I’m here, move around me!” In a subsonic flow, these waves can travel upstream and influence the flow well before it reaches the object. This is why the flow can smoothly divert around it.

Now, let’s see what happens as we increase our Mach number.

The Five Regimes of Flight

The Mach number neatly categorizes flow into distinct regimes, each with its own unique physics.

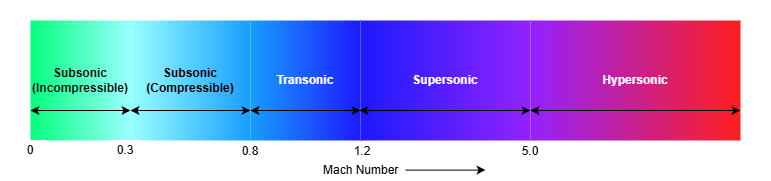
1. Subsonic Incompressible (M < 0.3)

• Compressibility: Negligible. Density changes are insignificant. The fluid is accurately treated as incompressible.
• Behavior: Pressure waves propagate freely upstream, allowing the flow to smoothly divert around objects. This is the realm of classic, low-speed aerodynamics.
• CFD Tip: For these flows, you can safely use the constant density assumption. The Pressure-Based solver in ANSYS Fluent is typically your most efficient and robust choice.

2. Subsonic Compressible (0.3 < M < 0.8)

• Compressibility: Significant. Density can no longer be considered constant. As the flow accelerates, it expands and its density drops, even before reaching the speed of sound.
• Behavior: While still subsonic, the flow exhibits measurable compressibility effects, such as an increase in drag and changes in pressure distribution compared to incompressible theory.
• CFD Tip: You must now use a compressible formulation, typically an ideal gas law for density. The Pressure-Based solver remains highly effective for this regime, but it must now solve the energy equation to account for density changes.

3. Transonic (0.8 < M < 1.2)

• The Grey Area: This is where things get truly interesting. The flow is a mixed bag—subsonic in some areas and supersonic in others.
• Behavior: As the flow accelerates over a surface (like an airplane wing), it can locally exceed Mach 1. This creates shock waves, which are sharp, discontinuous jumps in pressure, temperature, and density. These shocks cause a dramatic increase in drag (“wave drag”).
• Iconic Feature: The “transonic drag rise.”

4. Supersonic (1.0 < M < 5.0)

• Compressibility: Dominant. The fluid is highly compressible.
• Behavior: The object is moving faster than its own pressure waves. Those “get out of the way” signals cannot travel upstream. The fluid ahead has no idea the object is coming until it’s too late. This leads to the formation of a shock wave angled away from the object. The flow must pass through this shock to get out of the way.
• CFD Tip: This is the primary domain of the Density-Based solver, which is specifically designed to handle these sharp shocks and strong density gradients.

5. Hypersonic (M > 5.0)

High-Temperature Effects: The shock layer becomes incredibly hot, leading to significant heat transfer to the vehicle (this is a primary design challenge for re-entry vehicles).

Extreme Physics: At these incredible speeds, new physical phenomena emerge that aren’t present at lower Mach numbers.

Behavior: The energy involved is so high that it can cause:

Real Gas Effects: Molecular vibration, dissociation, and ionization.

Why Does This Matter for Your CFD Simulation?

Understanding the Mach number of your flow isn’t just academic—it dictates your entire CFD setup.

1. Solver Choice: As discussed in our previous post on Fluent Solvers, the Mach number is the primary driver for choosing between Pressure-Based and Density-Based solvers.
2. Material Properties: For compressible flows (M > 0.3), you must use an ideal gas or real gas model for density instead of constant density.
3. Boundary Conditions: Inlet and outlet conditions need to be set carefully. For supersonic inlets, all flow variables must be prescribed. For supersonic outlets, pressure should not be specified.
4. Shock Capturing: Resolving shocks requires specific numerical schemes (e.g., 2nd Order Upwind) and often mesh refinement in regions where shocks are expected.

The Bottom Line

The Mach number is more than just a number—it’s a passport to different worlds of fluid behavior.

• M < 0.3: You’re in simple, incompressible territory.
• M > 0.3: Compressibility starts to become significant. Your CFD model must account for changing density.
• M > 1.0: You’ve broken the sound barrier. Welcome to the world of shock waves, sonic booms, and a whole new set of CFD challenges.

So, the next time you set up a simulation, ask yourself: “What’s my Mach number?” The answer will guide you toward an accurate and efficient solution.

---

Got a specific compressible flow problem you’re trying to model? Struggling with convergence in a transonic case? Share your challenges in the comments below!

Further Reading:

• Understanding Fluent Solvers: Pressure-Based vs Density-Based