Have you ever wondered why honey pours downs so smoothly in a steady manner and water from your tap just swirls and splashes (not well-behaved at all)? Well, someone might say its one word answer is VISCOSITY and he/she will not be wrong. Honey is around 2000 times more viscous compared to water on average and it does help in that. Then why does water flowing slowly through a pipe also seem to have order? Is there more to it? In short YES! Let’s break down the concept of laminar and turbulent flows.
Laminar Flow: The Order
Picture a stack of pancakes, one perfectly aligned over another. Now, you gently pour syrup over it and it neatly flows over the pancakes in clean, parallel sheets. That’s laminar flow in action:
- Smooth
- Predictable
- Layers slide past each other with little mixing
Examples IRL?
- Pouring a layer of oil gently over water in a container
- Smoke from an incence stick before it starts dancing around
- Blood flow in viens (not arteries) under normal conditions
The term “LAMINAR” (derived from the word ‘laminae’ which means layers or sheets) just means that nature has divided the stack of fluid into layers or sheets which slide one over another with minimal mixing.

Turbulent Flow: The Rock Concert
Now, imagine your little cousin runs in and shakes plate or starts drumming the pancakes with a spoon, the syrup splashes and swirls, twists in all directions. It’s none other than turbulent motion.
- Chaotic
- Swrling eddies and vortices
- Lots of energy and mixing
Examples IRL?
- Water gushing out of a tap at high speed
- Smoke from that incence swirling after it reaches a certain height
- Airflow around a speeding car

Reynold’s Number: The Decision Maker
Reynolds Number (Re) is a dimensionless number that decides if a flow is laminar or turbulent. Dimensionless implies it does not have any unit, just a magnitude which is immensely important for fluid mechanics.
It is the ratio of the inertial force to the viscous force; it is a measure of how strong the inertial force of the flow is compared to its viscous force.
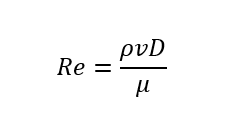
where,
rho (Greek letter): average density of the fluid
v : average velocity of the flow
D : characteristic length (depends on the geometry of the flow conditions)
mu (Greek letter) : dynamic viscosity of the fluid
- Low Reynolds number (Re < transition value) : Fluid stays calm (laminar).
- High Reynolds number (Re > transition value): Fluid gets rowdy (turbulent).
But what is this charcteristic length? How is it decided based on the geometry?
Well, this question haunted me a lot too. But after my fair share of experiences what I have understood is it is essentially the length over which velocity gradients are significant and viscous effects interact with the flow.
- For flow in a pipe, D: diameter of the pipe
- For flow over a flat plate, D is the distance from the leading edge i.e., the distance from the front edge of the plate where the flow starts to the point on the plate where Re is being measured.
- For flow around a sphere, D is the diameter of the sphere.
- For airfoil or car bodies, D is usually the chord length or a representative body length.
Critical Reynolds Number: The Transition Phase
Now lets discuss the transition values. It is the point where the flow stops being laminar and slowly switches to turbulent.
Its not fixed but depends on:
- Geometry of the flow
- Surface Roughness
- External disturbances in the flow
- Geometry of the flow:
In case of a flow through a pipe, the transition happens between Re values 2000-4000.
Similarly for incase of a flow over a flat plate, the transition takes place around 5*10^5 Re.
This is because the type of geometry influences the boundary layer development.
2. Surface Roughness:
Rough surfaces promote earlier transition (trigger turbulence at lower Reynolds numbers).
Smooth surfaces delay transition since disturbances have to grow more before turbulence sets in.
3. External disturbances in the flow:
External vibrations, noise, or upstream turbulence can cause earlier transition.
- A perfectly controlled laboratory experiment might show later transition.
- Real-world flows with unavoidable disturbances often transition earlier.
This is why we say the critical Reynolds number is approximate and context-specific.
Let’s conclude
| Feature | Laminar Flow | Turbulent Flow |
| Appearance | Smooth layers | Chaotic swirls |
| Reynolds Number | Low | High |
| Mixing | Minimal | HIgh |
| Energy Loss | Less | More |
| Example | Honey drip | River rapids |
So, next time you watch cream swirl in your coffee or see air stream past a speeding car, you’ll know whether you’re witnessing laminar calm or turbulent excitement and you’ll have a little insight into the secret life of fluids.
